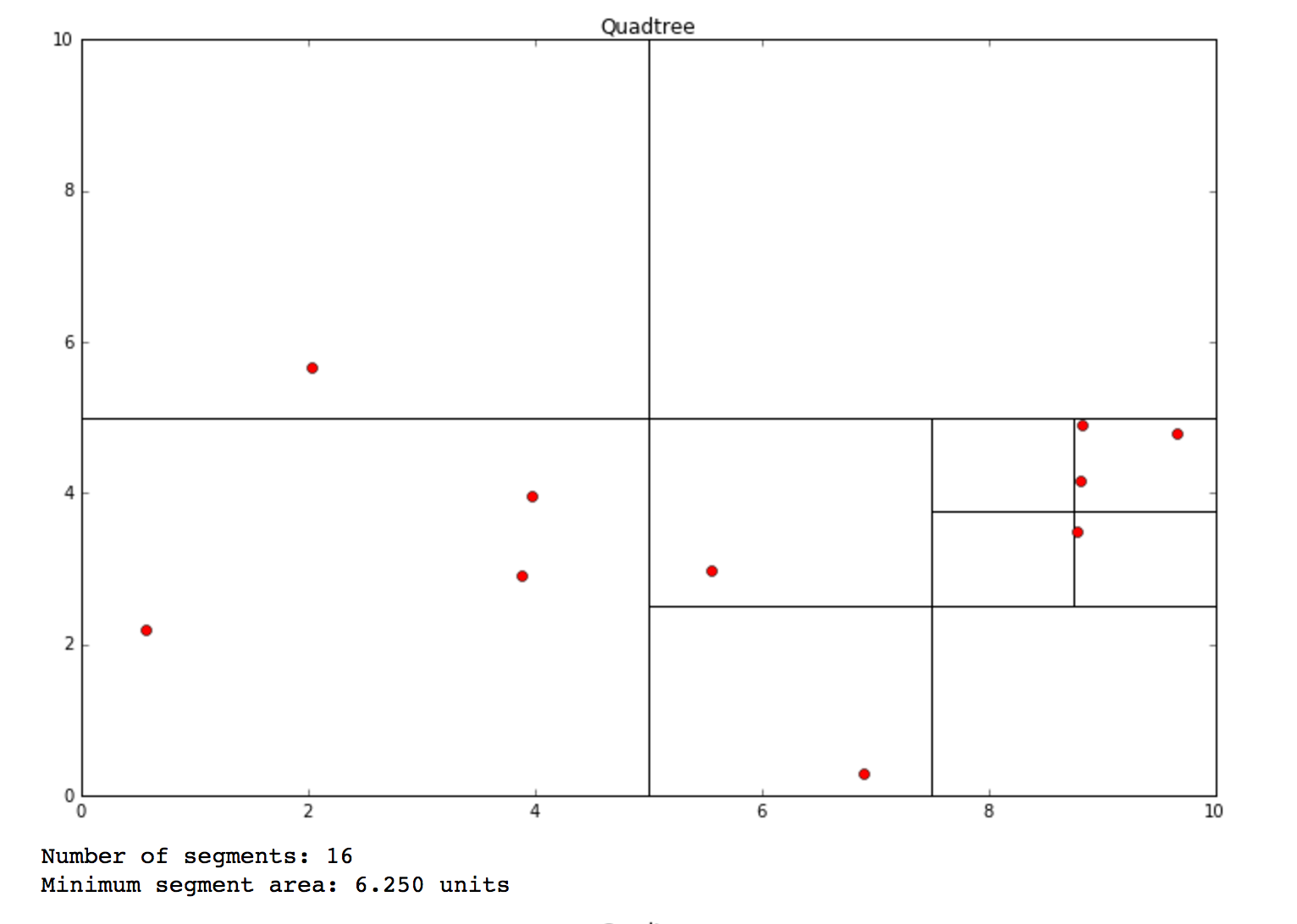
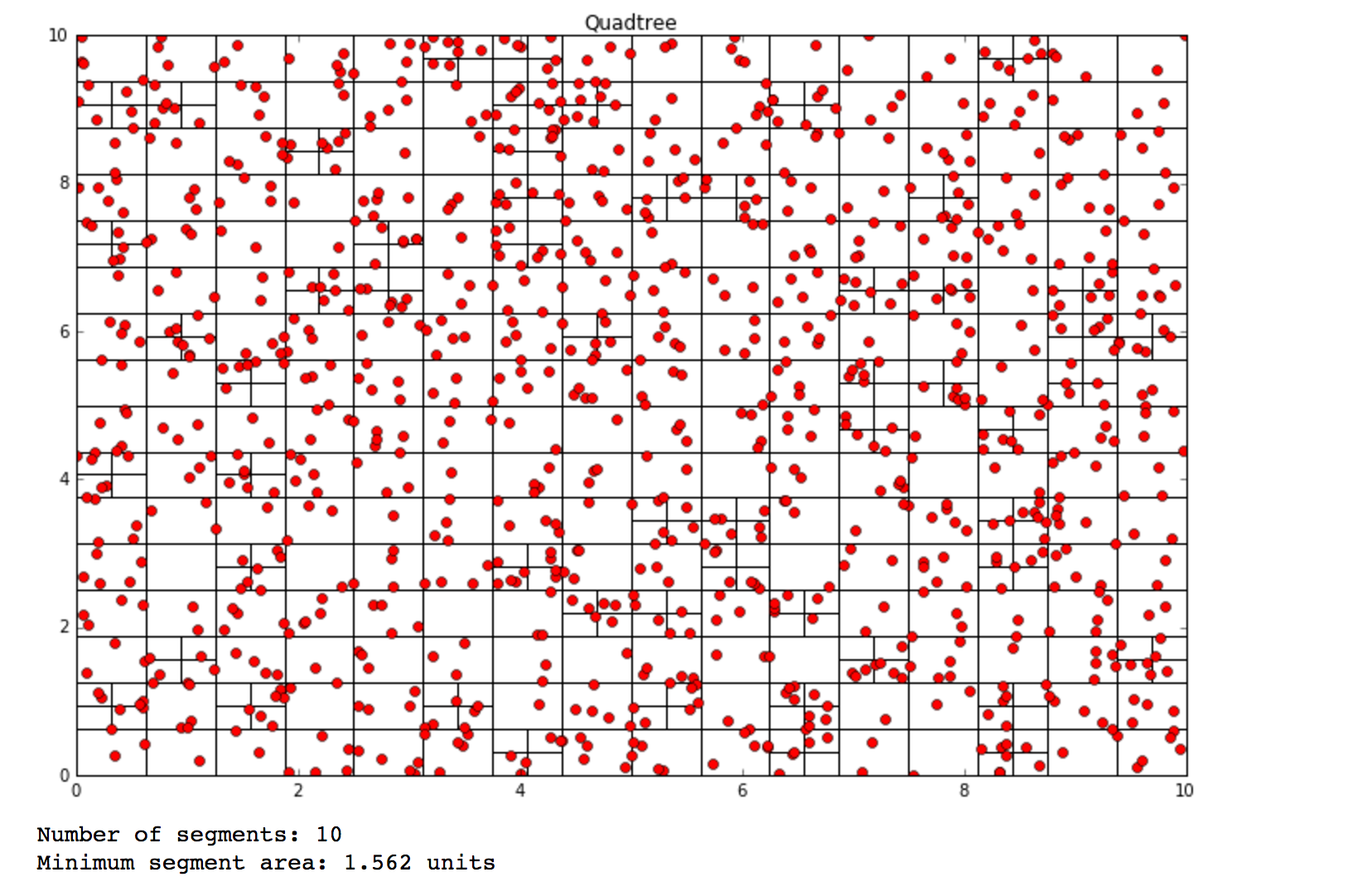
A quadtree is a data structure that can be useful for spatial indexing (it's often used in games for collision detection). In a quadtree, each node has exactly 4 children. When the number of nodes in a leaf reaches a specified threshold, the tree recursively divides. A tree representation might look something like this:
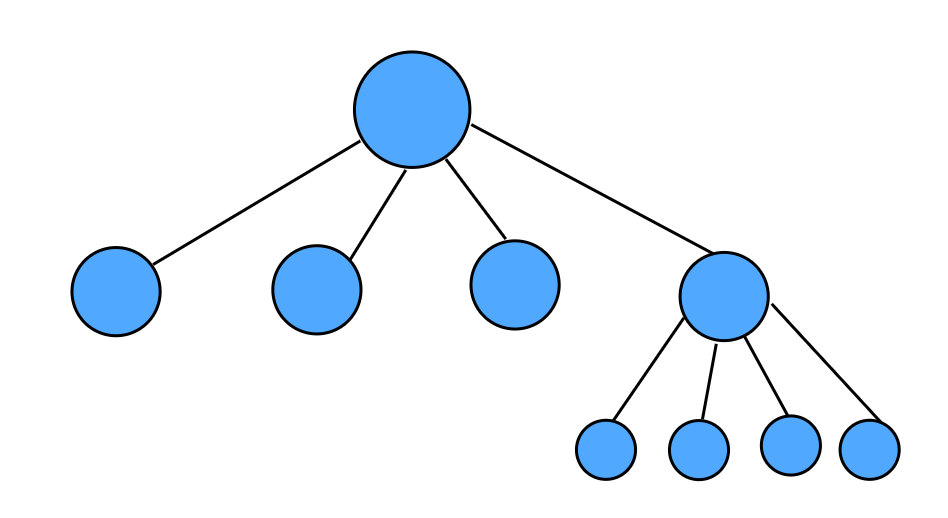
There are many ways to implement a quadtree, but I will explain my own methodology here.
Classes
To make my quadtree, I created 3 classes: Point, Node, and QTree. Point is the most simple: all we need are x and y coordinates.
class Point():
def __init__(self, x, y):
self.x = x
self.y = yThe next class is Node. Node objects need to be able to store points so that when the number of points reaches a specified limit, the tree will subdivide. I also want to be able to draw my quadtree in 2D space, so I must set starting x and y values, as well as a width and height.
class Node():
def __init__(self, x0, y0, w, h, points):
self.x0 = x0
self.y0 = y0
self.width = w
self.height = h
self.points = points
self.children = []
def get_width(self):
return self.width
def get_height(self):
return self.height
def get_points(self):
return self.pointsThe final class is the QTree class.
class QTree():
def __init__(self, k, n):
self.threshold = k
self.points = [Point(random.uniform(0, 10), random.uniform(0, 10)) for x in range(n)]
self.root = Node(0, 0, 10, 10, self.points)
def add_point(self, x, y):
self.points.append(Point(x, y))
def get_points(self):
return self.points
def subdivide(self):
recursive_subdivide(self.root, self.threshold)
def graph(self):
fig = plt.figure(figsize=(12, 8))
plt.title("Quadtree")
ax = fig.add_subplot(111)
c = find_children(self.root)
print "Number of segments: %d" %len(c)
areas = set()
for el in c:
areas.add(el.width*el.height)
print "Minimum segment area: %.3f units" %min(areas)
for n in c:
ax.add_patch(patches.Rectangle((n.x0, n.y0), n.width, n.height, fill=False))
x = [point.x for point in self.points]
y = [point.y for point in self.points]
plt.plot(x, y, 'ro')
plt.show()
returnQTree calls 3 helper methods.
def recursive_subdivide(node, k):
if len(node.points)<=k:
return
w_ = float(node.width/2)
h_ = float(node.height/2)
p = contains(node.x0, node.y0, w_, h_, node.points)
x1 = Node(node.x0, node.y0, w_, h_, p)
recursive_subdivide(x1, k)
p = contains(node.x0, node.y0+h_, w_, h_, node.points)
x2 = Node(node.x0, node.y0+h_, w_, h_, p)
recursive_subdivide(x2, k)
p = contains(node.x0+w_, node.y0, w_, h_, node.points)
x3 = Node(node.x0 + w_, node.y0, w_, h_, p)
recursive_subdivide(x3, k)
p = contains(node.x0+w_, node.y0+h_, w_, h_, node.points)
x4 = Node(node.x0+w_, node.y0+h_, w_, h_, p)
recursive_subdivide(x4, k)
node.children = [x1, x2, x3, x4]
def contains(x, y, w, h, points):
pts = []
for point in points:
if point.x >= x and point.x <= x+w and point.y>=y and point.y<=y+h:
pts.append(point)
return pts
def find_children(node):
if not node.children:
return [node]
else:
children = []
for child in node.children:
children += (find_children(child))
return children